Tags:
For a more thorough treatment on hyperbolic models, check out the initial theory by Daina Taimiða. Here is my summary (read: the parts I find coolest).
So to start with, there are 3 "geometries" that are possible in 2 dimensions. The first is called Euclidean geometry, and it's the one that humans actually use and care about. All the stuff you learned in school applies here: lines are straight, the angles of a triangle always add up to 180°, and there is only one possible way to make a parallel line some certain distance away from another line. That's all fine and dandy.
Now, grab or imagine a globe. Consider the following path:
In the end, you should have a path like this:
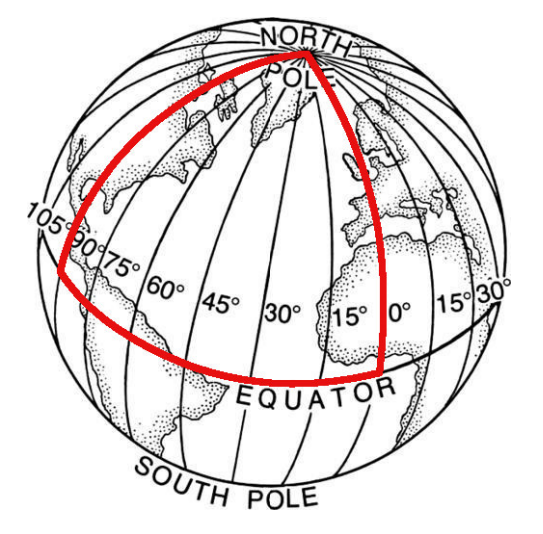
We see that this is a triangle with three straight sides, and three right angles. But, adding up the angles of this triangle gives us 270°, which is more than the 180 degrees that we expect from normal Euclidean geometry! Therefore, we must be in some different type of geometry. Naturally, we call it "spherical geometry." In spherical geometry, the angles of all triangles will add up to at least 180°.
Another property of spherical geometry is that there are no parallel lines! Due to the restrictions of the geometry, lines can only exist as circles that have the same radius as the sphere itself. So, the equator is a valid line, but a little circle contained entirely inside the Northern hemisphere would not be considered a line. So, in our example, there is no possible line that is parallel to the equator! Strange stuff.
Now we can move on to hyperbolic geometry. What should we expect? Well, in normal Euclidean geometry, we know that there is exactly one parallel line at a certain distance from a given line. If we move to spherical geometry, that rule is broken: there are no such things as parallel lines there. So, if we move into hyperbolic geometry, we break this rule in the other "direction" -- there are now infinitely many parallel lines to a given line!

This here is a model of that. Although, first, you may be wondering if these red lines are indeed lines. We can check that by folding our model in half, just as folding a piece of paper (a model of Euclidean space) makes a perfect line!

See? The red line goes exactly along this fold. That's actually how I plotted it: by folding where I wanted it to go, then sewing along the fold.
We see that there are three lines in the model.

The top one is our given line. If we wanted to make a parallel line that goes through point P, we see that there are two options that satisfy what we want:
Since the bottom two satisfy all these, they are both parallel to the top line. In fact, there are an infinite number of lines that are between the two candidates, so we see that there are indeed an infinite number of parallel lines!
Now, we move on to the last (interesting) property: the angles of triangles.

We see that in spherical geometry, the sum of the angles of a triangle S satisfies 180°<S<900° (where 900° comes from the 3 full angles at 360° each, minus the regular 180° from a "normal" triangle). In "normal" Euclidean geometry, we have S=180°. So, finally, in hyperbolic geometry, we see that S satisfies 0°<S<180°! So, it is possible to have a triangle in hyperbolic space with all three angles with measures of virtually 0°. This is what the reverse of my crochet model shows: as the three points of the triangle tend outwards towards infinity, their measures approach 0°, while the overall shape stays roughly fixed.